Diese Seite funktioniert nur mit Javascript.
Erlös-, Grenzerlösfunktion4.2.1.3 Cournotscher PunktIneffizienz und Wohlfahrtsverlust
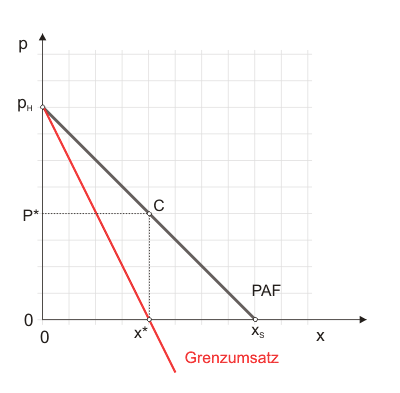
er Cournotsche Punkt zeigt die für den Monopolisten gewinnmaximierende Preis-Mengenkombination, wenn man so will seinen "Angebotspunkt". Im Mineralwassermonopol* teilt der Cournotsche Punkt C also die Preis-Absatz-Funktion in zwei gleiche Teile. Der Monopolist maximiert seinen Gewinn, wenn er den halben Prohibitivpreis $p_H$ verlangt bzw. die halbe Sättigungsmenge $x_S$ anbietet (s. Abbildung 1).
Solange ein weiterer Liter Mineralwasser den Umsatz noch steigen lässt (d.h. der Grenzumsatz positiv ist), und sei es nur um einen Cent, bietet der Monopolist ihn an. Das würde er aber nicht tun, wenn er jeden Liter selbst in Flaschen abfüllen müsste. Würde ihn dies pro Flasche 10 Cent kosten (Kosten einer Flasche plus Arbeitsleistung), dann würde er keinen weiteren Liter anbieten, wenn dieser den Umsatz um 9 Cent oder weniger steigen ließe. Um zu ermitteln, welche Menge seinen Gewinn maximiert, wenn die Produktion Kosten verursacht, wird die Gewinngleichung nach der Menge differenziert und null gesetzt:
$$ G(x) = U(x) - C(x) \tag{1} $$ $$ \cfrac{\text{d}G(x)}{\text{d}x} = \cfrac{\text{d}U(x)}{\text{d}x} - \cfrac{\text{d}C(x)}{\text{d}x} {\overset{!}{=}} 0 \tag{2} $$Daraus folgt als notwendige Bedingung für die Maximierung des Gewinns
$$ \underbrace{\cfrac{\text{d}U(x)}{\text{d}x}}_{\text{Grenzumsatz}} = \underbrace{\cfrac{\text{d}C(x)}{\text{d}x}}_{\text{Grenzkosten}} \tag{3} $$die Übereinstimmung von Grenzumsatz und Grenzkosten. Demnach lautet die Devise für den Monopolisten:
Dies ist das Gesetz des erwerbswirtschaftlichen Angebots, in dem das Gesetz des erwerbswirtschaftlichen Konkurrenzangebots als Spezialfall enthalten ist. Die Preis-Grenzkosten-Regel ergibt sich aus der Grenzumsatz-Grenzkosten-Regel (3), wenn die direkte Preiselastizität der Nachfrage gegen unendlich geht*:
$$ \underbrace{p}_{\text{Preis}} = \underbrace{\cfrac{\text{d}C(x)}{\text{d}x}}_{\text{Grenzkosten}} \tag{4} $$Natürlich macht die Devise, die Produktion auszudehnen, bis Grenzumsatz und Grenzkosten übereinstimmen, nur Sinn, wenn die Grenzumsätze über den Grenzkosten liegen. Entsprechend findet man in der hinreichenden Bedingung für ein Gewinnmaximum
$$ \cfrac{\text{d}^2G(x)}{\text{d}x^2} = \cfrac{\text{d}^2U(x)}{\text{d}x^2} - \cfrac{\text{d}^2C(x)}{\text{d}x^2} {\overset{!}{<}} 0 \tag{5} $$ $$ \cfrac{\text{d}^2U(x)}{\text{d}x^2} < \cfrac{\text{d}^2C(x)}{\text{d}x^2} \tag{6} $$die Information, dass die Steigung der Grenzumsätze unter der Steigung der Grenzkosten liegen muss. Wenn ausgangs die Grenzumsätze über den Grenzkosten liegen, nähern sie sich nämlich bei einer Ausdehnung der Produktion einander an (wenn die Grenzumsätze langsamer steigen als die Grenzkosten).
Auch hier ist die hinreichende Bedingung für die Gewinnmaximierung im Konkurrenzfall wieder als Spezialfall enthalten. Die zweite Ableitung der Umsatzfunktion ist dort gleich null, so dass sich (6) im Konkurrenzfall auf die Bedingung steigender Grenzkosten vereinfachen würde. Im Monopolfall ist die Bedingung aber weniger streng. Auch bei konstanten Grenzkosten kann ein (inneres) Gewinnmaximum vorliegen. Die Grenzumsätze müssen dann allerdings fallen, was aber ohnehin die Regel ist.
Die Herleitung verwendet allein die Definition für den Gewinn, der aus einer beliebigen Aktivität resultieren mag, bei der es sich nicht notwendigerweise um das Produzieren und Verkaufen von Gütern und Dienstleistungen handeln muss:
Mit dieser Regel - vollkommene Information vorausgesetzt - macht man auch nichts verkehrt, wenn man im Supermarkt entscheidet, welche Mengen man stiehlt*, oder kalkuliert, über welchen Zeitraum man eine Partnerschaft noch aufrecht erhalten sollte*. Da bei solchen Problemen der Zufall jedoch eine entscheidende Rolle spielt, sollte die Analyse sinnvollerweise Unsicherheit berücksichtigen. Das Resultat lautete dann allerdings ganz ähnlich:
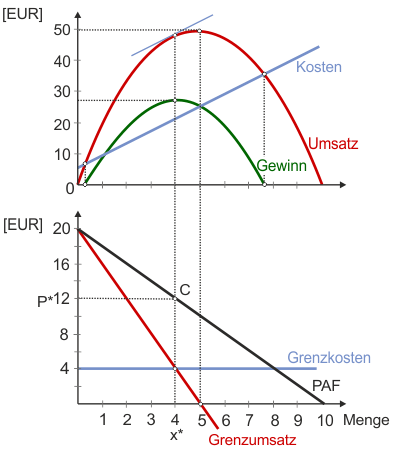
Das folgende Zahlenbeispiel - dargestellt in Abbildung 2 - geht vom eben erwähnten Fall konstanter Grenzkosten aus. Die Preis-Absatz-Funktion sei gegeben durch
$$ p = 20 - 2x \tag{7} $$und die Kostenfunktion laute:
$$ C = 5 + 4x \tag{8} $$Die notwendige Bedingung für ein Gewinnmaximum lautet
$$ 20 - 4x = 4 \tag{9} $$woraus man die gewinnmaximierende Menge $x^*$ zu 4 bestimmt. Mit der Preis-Absatz-Funktion bestimmt man die optimale Preisforderung $p^*$ des Monopolisten zu 12. Die hinreichende Bedingung ist erfüllt, denn die Grenzumsätze fallen, während die Grenzkosten konstant sind. Der Punkt $(x^*, p^*) = (4,12)$, der im unteren Teildiagramm mit C gekennzeichnet ist, ist der Cournot'sche Punkt. Er liegt immer auf der PAF. Der Schnittpunkt von Grenzumsatz- und -kostenfunktion bestimmt zwar die horizontale Position des Cournot'schen Punktes, hat aber keinen Namen. Warum auch immer es so sein mag: Es gilt als Zeugnis großer Unkenntnis, diesen Schnittpunkt mit dem Cournot'schen Punkt zu verwechseln.
In Tabelle 1, die das Zahlenbeispiel für ganzzahlige Produktionsmengen von 1 bis 10 zeigt, kann man beobachten, dass der Gewinn steigt, solange die Grenzumsätze über den Grenzkosten liegen. Das Maximum ist erreicht, wenn Grenzumsätze und Grenzkosten übereinstimmen.
| Tabelle 1 | ||||||
| Menge
|
Preis
|
Umsatz
|
Grenz-
umsatz |
Kosten
|
Grenz-
kosten |
Gewinn
|
| 1,00
|
18,00
|
18,00
|
16,00
|
9,00
|
4,00
|
9,00
|
| 2,00
|
16,00
|
32,00
|
12,00
|
13,00
|
4,00
|
19,00
|
| 3,00
|
14,00
|
42,00
|
8,00
|
17,00
|
4,00
|
25,00
|
| 4,00
|
12,00
|
48,00
|
4,00
|
21,00
|
4,00
|
27,00
|
| 5,00
|
10,00
|
50,00
|
0,00
|
25,00
|
4,00
|
25,00
|
| 6,00
|
8,00
|
48,00
|
-4,00
|
29,00
|
4,00
|
19,00
|
| 7,00
|
6,00
|
42,00
|
-8,00
|
33,00
|
4,00
|
9,00
|
| 8,00
|
4,00
|
32,00
|
-12,00
|
37,00
|
4,00
|
-5,00
|
| 9,00
|
2,00
|
18,00
|
-16,00
|
41,00
|
4,00
|
-23,00
|
| 10,00
|
0,00
|
0,00
|
-20,00
|
45,00
|
4,00
|
-45,00
|
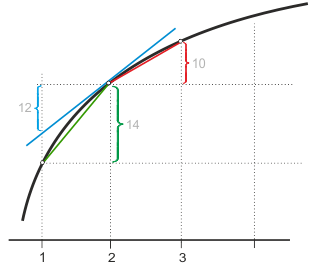
Warum stimmt der in Tabelle 1 ausgewiesene Grenzumsatz nicht mit der Differenz überein, die man aus den ausgewiesenen Umsatzwerten berechnet? Warum ist also z.B. bei der Menge 2 ein Grenzumsatz von 12 angegeben, obwohl der Umsatz beim Sprung von der Menge 1 auf die Menge 2 von 18 auf 32, also um 14 Einheiten steigt? Wenn man die Menge um eine Einheit erhöht, dann steigt der Umsatz doch gerade um den Grenzumsatz. So ist dieser doch definiert, oder?
Ja, das stimmt, allerdings nur näherungsweise. Wenn der Umsatz mithilfe der Grenzumsatzfunktion $GU=20-4x$ berechnet wird, ergeben sich die in der Tabelle ausgewiesenen Werte. Die Berechnung unterstellt infinitesimale Änderungen. Zwischen den in der Tabelle ausgewiesenen Produktionsmengen 1, 2, 3 ... liegen aber "große" Sprünge. Die Mengenänderung von 1 auf 2 ist alles andere als infinitesimal. Immerhin verdoppelt sich die Menge - eine Steigerung um 100 Prozent.
Wird die Menge von 1 auf 2 erhöht, dann bestimmt man aus der Differenz der Umsätze einen Grenzumsatz von 14. Nähert man sich aber von der anderen Seite aus an, wird also die Menge von 3 auf 2 zurückgenommen, dann würde man eine Umsatzänderung von absolut 10 bestimmen (=42-32). Die Abbildung zeigt mit der Steigung der blauen Gerade das Ergebnis, das man mithilfe der Grenzumsatzformel erhält, während die Steigungen der grünen und roten Gerade die schrittweise berechneten Grenzumsätze zeigen.
Nach ähnlichen Seiten im WWW suchen